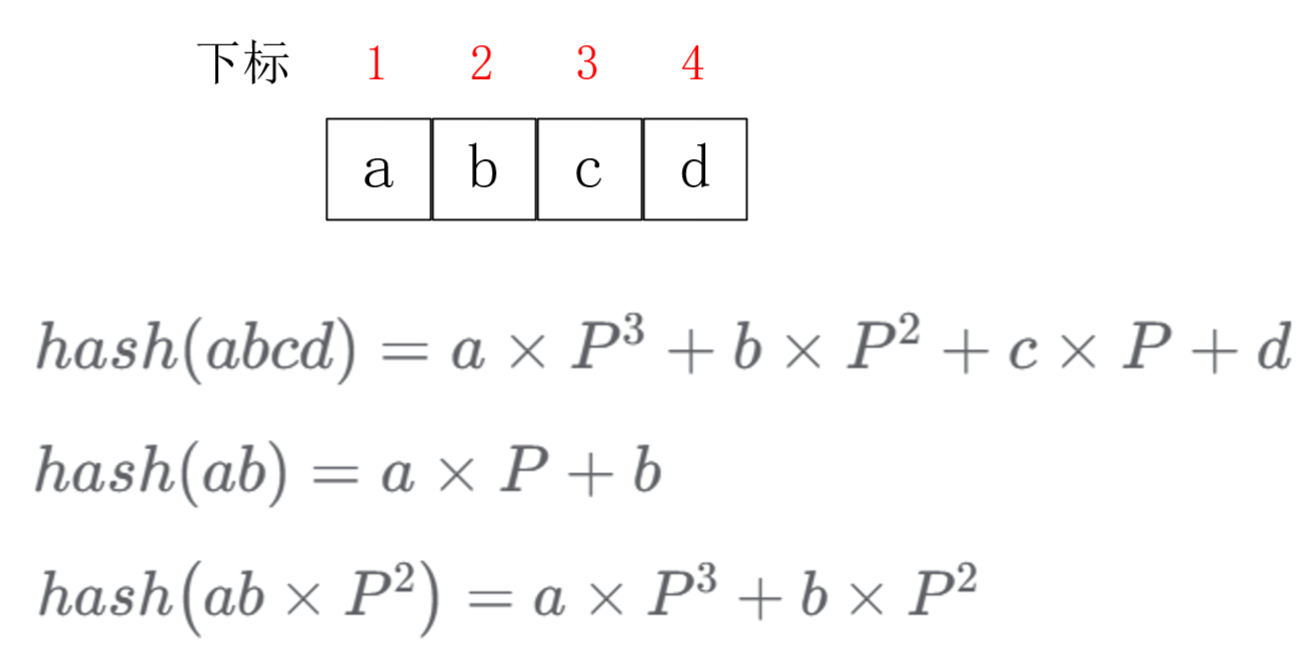数据结构模板

1.链表

1.1 静态链表（数组模拟）

1.1.1 单链表

#include <iostream>
using namespace std;
const int N = 100010;
int e[N], ne[N], idx, head = -1;

void add_head(int v)
{
    e[idx] = v, ne[idx] = head, head = idx++;
}

void add(int k, int v)
{
    e[idx] = v, ne[idx] = ne[k], ne[k] = idx++;
}

void remove(int k)
{
    if(~k) ne[k] = ne[ne[k]];
    else head = ne[head];
}

int main()
{
    int m;
    cin >> m;
    while(m --)
    {
        int k, v;
        char c;
        cin >> c;
        switch(c)
        {
            case 'H':
                cin >> v;
                add_head(v);
                break;
            // 题中对于k的计数从1开始，但是存储下标从0开始，因此需要k - 1
            case 'I':
                cin >> k >> v;
                add(k - 1, v);
                break;
            case 'D':
                cin >> k;
                remove(k - 1);
        }
    }
    for(int i = head; ~i; i = ne[i])
        cout << e[i] << " ";
    return 0;
}

注1：为了逻辑清晰代码简洁，无论是静态链表还是动态链表都最好加上头节点，但是仅在数组模拟单链表时没有头节点，因为算法题中使用单链表时一般仅使用在头插入新节点，不涉及其他操作，所以没有必要加入头节点

注2：在数组模拟单/双链表时在第k个位置之前/之后插入新节点，其中第k个位置是指按时间顺序依次插入的数即使删除了其中某些元素，这些被删除的元素依然占用位置(静态链表不会释放空间)。之所以没有像动态链表那样“在链表中第k个元素之前/之后插入”，是为了模板的简洁起见吧，静态链接一样可以在”在链表中第k个元素之前/之后插入”.

1.1.2 双链表

#include <iostream>
using namespace std;
const int N = 100010;
int e[N], l[N], r[N], idx;

void insert(int k, int v)  // 这里k是待插入节点左邻居的下标
{
    e[idx] = v;
    r[idx] = r[k], l[idx] = k;
    l[r[k]] = idx; r[k] = idx++; 
}

void remove(int k)  // 这里k是待删除节点的下标
{
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

int main()
{
    int m;
    cin >> m;
    r[0] = 1, l[1] = 0, idx = 2;
    
    while(m --)
    {
        string s;
        int k, v;
        cin >> s;
        
        if(s == "R")
        {
            cin >> v;
            insert(l[1], v);
        }
        else if(s == "L")
        {
            cin >> v;
            insert(0, v);
        }
        else if(s == "D")
        {
            cin >> k;
            remove(k + 1);            
        }
        else if(s == "IL")
        {
            cin >> k >> v;
            insert(l[k+1], v);
        }
        else if(s == "IR")
        {
            cin >> k >> v;
            insert(k+1, v);            
        }
    }
    for(int i = r[0]; i != 1; i = r[i])
        cout << e[i] << " ";
        
    return 0;
}

在数组模拟双链表中，使用了头节点和尾节点，来简化逻辑。

1.2 动态链表

1.2.1 单链表

struct LNode{
    int val;
    struct LNode *next;
};
typedef struct LNode* LinkList;

void add(int v, int k, LinkList head) //在第k个节点之后插入
{
    struct LNode *new_node;
    for(int i = 0; i < k; i++)
        head = head->next;
    new_node = (struct LNode*)malloc(sizeof(struct LNode));
    new_node->val = v;
    new_node->next = head->next;
    head->next = new_node;
}

void remove(int k, LinkList head) // 删除第k个节点
{
    for(int i = 0; i < k - 1; i++)  
        head = head->next;
        
    struct LNode *tmp;
    tmp = head->next;
    head->next = tmp->next;
    free(tmp);
}

int main()
{
    LinkList head = (struct LNode *)malloc(sizeof(struct LNode));
    head->next = NULL;
    
    int n, x;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> x;
        add(x, i, head);
    }
    
    LNode *p = head->next;
    while(p != NULL)
    {
        printf("%d ", p->val);
        p = p->next;
    }
    return 0;
}

包含头节点的动态单链表

1.2.2 双链表

#include <iostream>
using namespace std;
struct DNode{
    int val;
    struct DNode *l, *r;
};
struct DLinkList{
    struct DNode *lhead, *rhead;
    int cnt;
};

struct DNode* find(int k, DLinkList *h)
{
    struct DNode *p;
    if(k <= (h->cnt >> 1)) 
    {
        p = h->lhead;
        for(int i = 0; i < k; i++) p = p->r;
    }
    else
    {
        p = h->rhead;
        for(int i = 0; i <= (h->cnt - k); i++) p = p->l;
    }
    return p;
}

//假设左头节点的下标为0，k表示在第k节点之后插入一个新节点
void add(int v, int k, DLinkList* h)
{
    struct DNode *p = find(k, h);
    struct DNode *new_node = (struct DNode *)malloc(sizeof(struct DNode));
    new_node->val = v;
    new_node->l = p;  new_node->r = p->r;
    p->r->l = new_node;
    p->r = new_node;
    h->cnt ++;
}

//假设左头节点的下标为0，删除第k个节点
void remove(int k, DLinkList* h)
{
    struct DNode *p = find(k, h);
    p->l->r = p->r;
    p->r->l = p->l;
    free(p);
    h->cnt --;
}

int main()
{
    DLinkList* h = (struct DLinkList *)malloc(sizeof(struct DLinkList));
    h->lhead = (struct DNode *)malloc(sizeof(struct DNode));
    h->rhead = (struct DNode *)malloc(sizeof(struct DNode));
    h->lhead->r = h->rhead;
    h->rhead->l = h->lhead;
    h->cnt = 0;
    
    int n, x;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> x;
        add(x, i, h);
    }
    
    DNode *p = h->lhead->r;
    while(p != h->rhead)
    {
        printf("%d ", p->val);
        p = p->r;
    }
    return 0;
}

包含左右头节点的双链表

2.栈

// 数组模拟方式
int stk[N], tt;
if (op == "push")
{
    cin >> x;   stk[ ++ tt] = x;
}
else if (op == "pop") tt -- ;
else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;
else cout << stk[tt] << endl;


// STL方式
stack<int> stk;
if(op == "push") 
{
    cin >> x;   stk.push(x);
}
else if(op == "pop")  stk.pop();
else if(op == "empty") cout << (stk.size()? "NO" : "YES") << endl;
else cout << stk.pop() << endl;

2.1 单调栈

适用问题：求数组中某一元素左边/右边第一个比该元素本身大/小的元素

单调栈的定义：满足单调性的栈结构（从栈底到栈顶的元素依次递增/递减）

例如单调递增栈，在插入元素为为了满足栈的单调性，需要在尽可能弹出最少的元素下将其插入：

1 2	while(tt && stk[tt] > x) tt--; stk[++tt] = x;

时间复杂度：

首先，暴力求解该问题需要二重循环，时间复杂度为。而分析使用单调栈的时间复杂度，每一个元素最多会入栈一次和出栈一次，因此内层时间复杂度为，整体时间复杂度为

2.1.1 例题

原题链接：单调栈 - AcWing题库

求数组中某一元素左边第一个比该元素本身小的元素

#include <iostream>
using namespace std;
const int N = 100010;
int stk[N], tt;

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        while(tt && stk[tt] > x) tt--;
        if(tt) printf("%d ", stk[tt]);
        else printf("-1 ");
        stk[++tt] = x;
    }
    return 0;
}

3.队列

// 数组模拟方式
int q[N], hh, tt = -1;
if(s == "push")
{
	cin >> x;  q[++tt] = x;
}
else if(s == "pop")    hh++;
else if(s == "query")  cout << q[hh] << endl;
else
{
	if(hh <= tt)  cout << "NO" << endl;
	else    cout << "YES" << endl;
}

// STL方式
queue<int> q;
if(s == "push")
{
    cin >> x; q.push(x);
}
else if(s == "pop")  q.pop();
else if(s == "query") cout << q.front() << endl;
else 
{
    if(q.size()) cout << "NO" << endl;
    else   cout << "YES" << endl;
}

3.1 单调队列

适用问题：求一个数组中滑动窗口中的最大/最小值

单调队列的定义：满足单调性的“双端“队列（从队首到队尾元素依次递增/递减）

例如单调递增队列，在向队尾插入元素时，需要在满足从队首到队尾元素单调递增的情况下，尽可能少的弹出队尾元素：

1 2	while(hh <= tt && q[tt] > a[i]) tt--; q[++tt] = a[i];

单调队列不是普通的队列，因为单调队列需要从队尾弹出元素，不满足FIFIO

时间复杂度：

假设数组的大小为，滑动窗口的大小为，如果暴力求解该问题则时间复杂度为。如果使用单调队列来解决该问题，同样每一个元素最多会入队一次和出队一次，所以总时间复杂度为

求解过程：

以使用非严格单调递增队列求滑动窗口中的最小值为例：

对于新滑入的元素，需要在满足从队首到队尾元素非严格单调递增的情况下，尽可能少的弹出队尾元素。
对于新滑出的元素，如果该元素和队头元素(或下标)的值相等，则弹出队头元素；如果该元素和队头元素(或下标)的值不等，则说明滑动窗口内存在比滑出元素更小的值，因此按照单调队列的定义，滑出元素已经出队。
对于每一个滑动窗口，单调队列的队头元素即为窗口内的最小值。

3.1.1 例题

滑动窗口 - AcWing题库

求滑动窗口内的最大值和最小值。

#include <iostream>
using namespace std;
const int N = 1000010;
int a[N], q[N], hh, tt = -1;

int main()
{
    int n, k;
    cin >> n >> k;
    for(int i = 0; i < n; i++)  cin >> a[i];
    
    for(int i = 0; i < n; i++)
        
    {
        while(hh <= tt && q[tt] > a[i])  tt--;      // 构建非严格单调递增队列
        q[++tt] = a[i];
        if(i - k >= 0 && q[hh] == a[i - k]) hh++;   //如果滑出元素是队头，则出队
        if(i + 1 >= k) printf("%d ", q[hh]);        // 输出队头元素
    }
    printf("\n");
    hh = 0, tt = -1;
    for(int i = 0; i < n; i++)
    {
        while(hh <= tt && q[tt] < a[i])  tt--;      // 构建非严格单调递减队列
        q[++tt] = a[i];
        if(i - k >= 0 && q[hh] == a[i - k]) hh++;   //如果滑出元素是队头，则出队
        if(i + 1 >= k) printf("%d ", q[hh]);        // 输出队头元素
    }
    return 0;
}

4.KMP算法

适用问题：求模式串P在一个字符串S中所有出现位置的起始下标

4.1 概念：

非平凡前缀：除最后一个字符外，一个字符串的全部头部组合；如”abab”，它的非平凡前缀有”a, ab, aba”
非平凡后缀：除第一个字符外，一个字符串的全部尾部组合；如”abab”，它的非平凡后缀有”b, ab, bab”
部分匹配值：前缀和后缀的最长共有元素的长度；如”abab”，它的部分匹配值是2，最长共有元素为”ab”。

部分匹配值表：记录模式串的所有前缀子串的部分匹配值的表，即next[]数组，例如模式串P”abababc”：

假设模式串P从下标1开始存储

下标	非平凡前缀	非平凡后缀	最长共有元素	部分匹配值
0	{}	{}	{}	ne[0] = 0
1	{}	{}	{}	ne[1] = 0
2	{a}	{b}	{}	ne[2] = 0
3	{a,ab}	{a,ba}	{a}	ne[3] = 1
4	{a,ab,aba}	{b,ab,bab}	{ab}	ne[4] = 2
5	{a,ab,aba,abab}	{a,ba,aba,baba}	{aba}	ne[5] = 3
6	{a,ab,aba,abab,ababa}	{b,ab,bab,abab,babab}	{abab}	ne[6] = 4
7	{a,ab,aba,abab,ababa,ababab}	{c,bc,abc,babc,ababc,bababc}	{}	ne[7] = 0

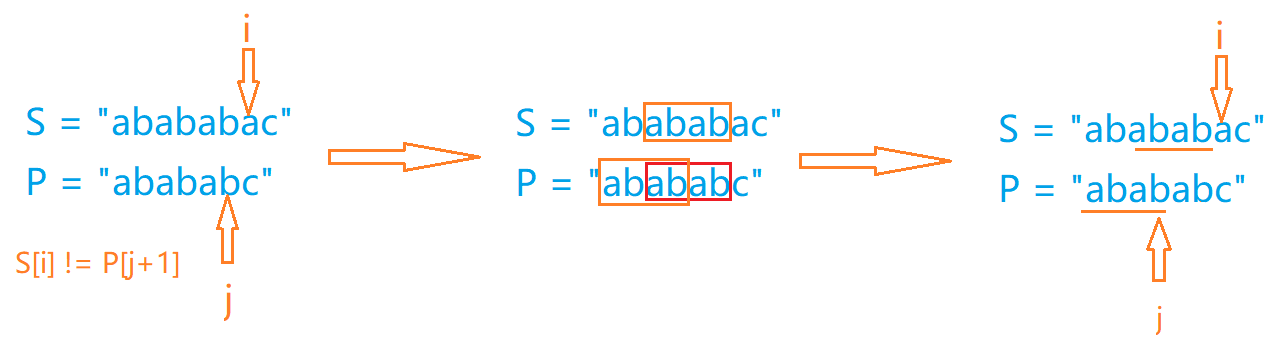
4.2 求部分匹配值表的意义：

举个例子，假设字符串S为”abababac”，模式串P为”abababc”：

在第二步时，可知S串和P串的已匹配子串相等，又根据部分匹配值表可知P串最长非平凡前缀和后缀共有子串，因此可知橙色框中的两个子串相等，从而再该位置继续进行模式匹配，尽可能减少匹配次数，从而降低时间复杂度。

4.3 KMP算法的代码实现：

从上面的介绍中可以总结KMP算法的求解分为两个主要步骤：

求部分匹配值表next[]数组
利用next[]数组进行字符串S和模式串P的匹配

这两个步骤的实现上几乎是一致的，步骤一需要进行模式串P的非平凡前缀和非平凡后缀的匹配，同时记录并利用ne[]数组，步骤二需要进行字符串S和模式串P的匹配，同时利用ne[]数组：

cin >> n >> p + 1 >> m >> s + 1;

// 1.求ne数组
for(int i = 2, j = 0; i <= n; i++)
{
    while(j && p[j + 1] != p[i]) j = ne[j];
    if(p[i] == p[j + 1]) j++;
    ne[i] = j;
}
// 2.进行字符串S和模式串P的匹配
for(int i = 1, j = 0; i <= m; i++)
{
    while(j && p[j + 1] != s[i]) j = ne[j];
    if(p[j + 1] == s[i]) j++;
    if(j == n)   // 成功匹配
    {
        printf("%d ", i - n);
        j = ne[j];
    }
}

4.4 KMP算法的时间复杂度

时间复杂度：

显然暴力求解该问题的时间复杂度为，而KMP算法将时间复杂度降为

简单证明：

KMP算法的两个步骤几乎是一致的，我们对步骤一求ne数组的过程进行分析：

for循环每一次增加1，而可能增加1，因此有；根据ne[i] = j，则，可知，换一个符号有；每一次循环中最多增加1，最多循环n次，而仅能通过j = ne[j]变小，因此可知while循环在整个循环过程中最多执行n次；所以，求ne[]数组的时间复杂度为。类似的，可知进行模板匹配的时间复杂度为

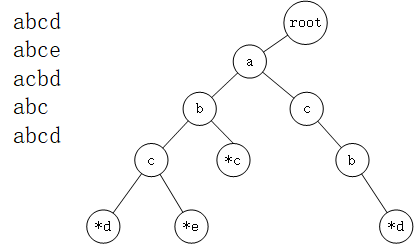
5.Trie树

适用问题：Trie树又称字典树、单词查找树。适用于字符串集合的的高效存储和快速查找。一般使用Trie树的场景字符的种类不会非常多，字符越少则重复的概率高，存储的效率也就高。

Trie树的图示：

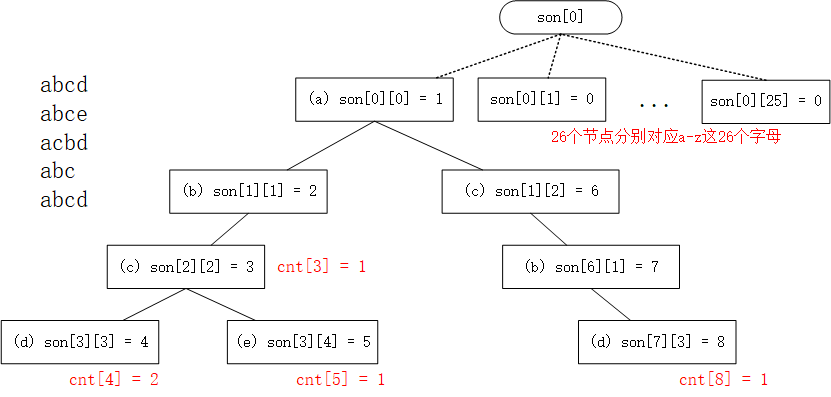
我们可以用数组模拟链表的思想来构造树。假设字符串中一共可能有k种类型的字符，则树存储类型son[i][k]，将下标0设置为头节点。此外，为了记录字符串的结束位置和个数，需要额外的记录数组cnt[N]。

模板如下：

int son[N][26], cnt[N], idx;
char str[N];
void add()
{
    int p = 0;
    for(int i = 0; str[i]; i++)
    {
        int v = str[i] - 'a';
        if(!son[p][v]) son[p][v] = ++idx;
        p = son[p][v];
    }
    cnt[p] ++;
}

int query()
{
    int p = 0; 
    for(int i = 0; str[i]; i++)
    {
        int v = str[i] - 'a';
        if(!son[p][v]) return 0;
        else p = son[p][v];
    }
    return cnt[p];
}

5.1 例题

最大异或对 - AcWing题库

想要存储所有整数，并求所有整数的异或对，应该以二进制来保存每一个数，则一共有两种字符，则适用Tire树来存储。

为了求最大异或对，高位比低位的贡献要大的多，显然我们需要从高位到低位依次来存储一个二进制数。

由于异或运算的性质，对于任意一个数，从高位到低位，查找相反的数(0查找1，1查找0)即为该数的最大异或对，查找次数为Trie树的高度，本题中为31次。

最后，本题的数据范围是，支持复杂度为的算法，因此对于分别求每一个数的最大异或对，取最大即可，总的时间复杂度为。

#include <iostream>
using namespace std;
const int N = 100010, M = 3000010;
int son[M][2], a[N], idx;

void add(int x)
{
    int p = 0;
    for(int i = 30; i >= 0; i--)
    {
        int v = (x >> i) & 0x01;
        if(!son[p][v]) son[p][v] = ++ idx;
        p = son[p][v];
    }
}

int find(int x)
{
    int p = 0, res = 0;
    for(int i = 30; i >= 0; i--)
    {
        int v = (x >> i) & 0x01;
        if(son[p][!v])
        {
            res += 1 << i;
            p = son[p][!v];
        } 
        else
            p = son[p][v];
    }
    return res;
}

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> a[i];
        add(a[i]);
    }
    int res = 0;
    for(int i = 0; i < n; i++)
        res = max(res, find(a[i]));
    
    cout << res << endl;
    return 0;
}

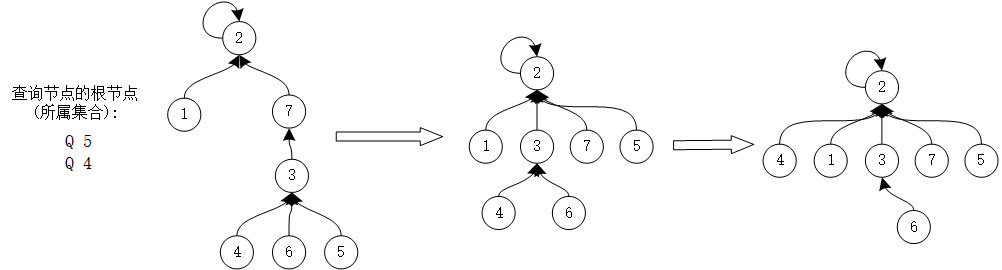
6.并查集

适用问题：高效的合并集合以及查找数据所属的集合关系。

时间复杂度：加入路径压缩之后，合并和查询的时间复杂度都近乎

6.1 并查集的模板和图示

初始化：

1 2	int p[N]; for(int i = 1; i <= n; i++) p[i] = i;

查询（未加入路径压缩）：

int find(int x)
{
    if(p[x] != x) return find(p[x]);
    return p[x];
}

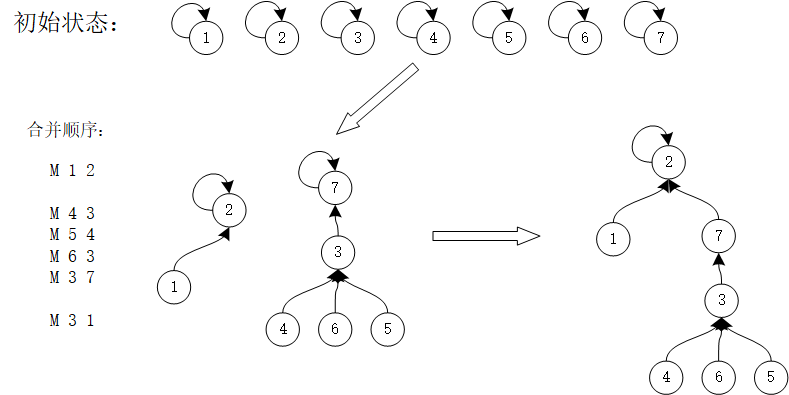
合并：

1	p[find(a)] = find(b);

图示：

查询（加入路径压缩）：

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

加入路径压缩之后，每一次调用find()函数，可能会使得子节点直接接在根节点下，如图：

6.1 带权并查集

朴素版本的并查集仅能够查询集合所属关系，如果集合内部点存在关系的话，则需要额外维护节点的边权信息。

一般用数组d[i]表示节点到其父节点的距离信息。

食物链 - AcWing题库

在本题中，节点之间存在有向依赖关系。我们可以用表示节点和其父节点之间的关系：0表示是同类，1表示是的天敌，2表示是的天敌。

参考题解：食物链(带权并查集) - AcWing

关系传递的本质是向量的运算

假设a的祖先为x，b的祖先是y，可表示为向量：，每一句话给出a和b的关系可以表示为：

若，说明a和b之间存在关系，由于，则；对3取模之后移动到正整数。此时0表示a,b为同类，1表示a吃b，2表示b吃a，直接与进行比较即可得出真伪
若，说明a和b之间不存在关系，则给出的关系一定是对的，合并p[x]=y，假设，则，即

#include <iostream>
using namespace std;
const int N = 50010;
int p[N], d[N];

int find(int x)
{
    int u;
    if(p[x] != x) 
    {
        u = find(p[x]);
        d[x] += d[p[x]];
        p[x] = u;
    }
    return p[x];
}

int main()
{
    int n, k;
    cin >> n >> k;
    for(int i = 1; i <= n; i++) p[i] = i;
    
    int res = 0;
    while(k --)
    {
        int t, a, b;
        cin >> t >> a >> b;
        if(a > n || b > n) { res ++; continue; }
        int rel;
        if(t == 1)  rel = 0;
        else rel = 1;
        int x = find(a), y = find(b);
        if(x == y)
        {
            if( ((d[a] - d[b]) %3 + 3) % 3 != rel) res ++;
        }
        else
        {
            p[x] = y;
            d[x] = d[b] + rel - d[a];
        }
    }
    cout << res << endl;
    
    return 0;
}

7.堆

7.1 堆的性质

堆是一棵完全二叉树（除了最后一层外所有层的节点都是非空的，最后一层从左到右都是满的）。以小根堆为例，满足父节点小于等于左右儿子的完全二叉树。

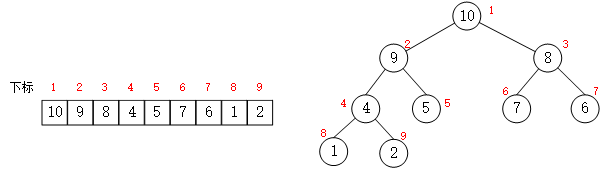
7.2 堆的数组存储方式

堆是一棵完全二叉树，因此，可以利用数组下标来表示堆节点的父子关系：

假设父节点的下标为，则左儿子的下标为，右儿子的下标为。因此，堆的数组存储需要从1开始存储。

7.3 堆的两个基本操作

**up()**：

代码：

void up(int u)
{
    while(u > 1 && h[u/2] > h[u])
    {
        swap(h[u/2], u);
        u /= 2;
    }
}

图示，对8所在节点执行up()操作：

down():

代码：

void down(int u)
{
    int t = u;
    if(u * 2 <= cnt && h[u*2] < h[t])  t = u * 2;
    if(u * 2 + 1 <= cnt && h[u*2+1] < h[t]) t = u * 2 + 1;
    if(u != t)
    {
        swap(h[u], h[t]);
        down(t);
    }
}

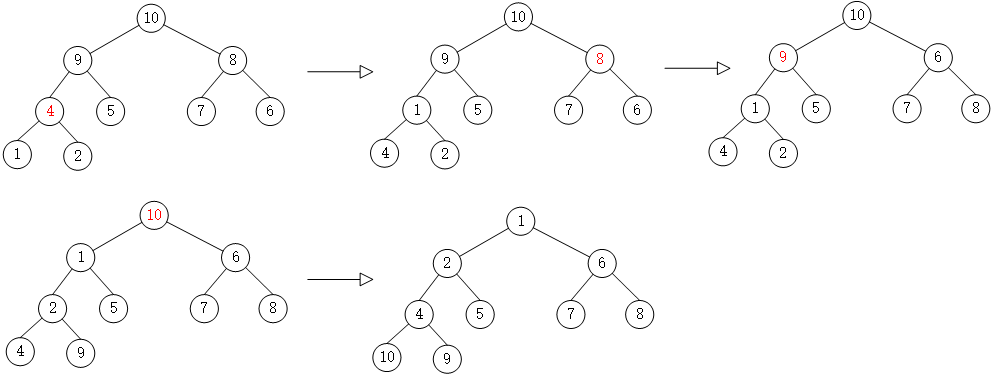
图示，对10所在节点执行down()操作：

7.4 堆的建立

代码：

1 2	for(int i = 1; i <= n; i++) cin >> heap[i]; for(int i = n / 2; i; i--) down(i);

图示（图中标红的节点为将要执行down操作的节点）：

时间复杂度分析：

1 2	for(int i = 1; i <= n; i++) cin >> heap[i]; for(int i = n / 2; i; i--) down(i);

简单证明为什么是而不是：

操作次数：

使用错位相减法计算差比数列可知

因此，总的时间复杂度为

7.5 堆支持的操作

插入一个数：heap[++cnt] = x; up(cnt);

求集合中的最小值：heap[1];

删除最小值：heap[1] = heap[cnt]; cnt--; down(1);

删除任意一个元素：heap[k] = heap[cnt]; cnt--; up(k); down(k);

修改任意一个元素：heap[k] = x; up(k); down(k);

8.哈希表

适用问题：高效的存储和查找值或者键值对

时间复杂度：如果哈希函数设计的很好，分布均匀几乎不产生冲突，那么存储和查找的期望时间复杂度为

哈希表的设计主要包括哈希函数的设计和解决冲突的方式。

哈希函数：采用取余法

1	int key = (x % N + N) % N;

一般处理的问题，数值都是随机的，则可以采用取余作为哈希函数。如果是非随机数列，则可以针对性的设计哈希函数来保证分布均匀。

模数取比hash数组规模稍大一点的质数，例如比的稍大的质数是，比稍大的质数是

拉链法：

拉链法将hash数组中每个元素视为一个链表的头节点；如果键产生冲突，就将值存储在键对应的链表中

const int N = 100003;
int e[N],ne[N],h[N],idx;
memset(h , -1 , sizeof h);

void insert(int x)
{
    int u = (x % N + N) % N;
    e[idx] = x , ne[idx] = h[u] , h[u] = idx++;
}

bool query(int x)
{
    int u = (x % N + N) % N;
    for(int i = h[u]; ~i ; i = ne[i])
        if(e[i] == x)  return true;
    return false;
}

开放寻址法：

当产生冲突时，开放寻址法会在键指向的位置后向右寻找空位来存储值

const int N = 200003, null = 0x3f3f3f3f;
int h[N];
memset(h, 0x3f, sizeof h);
int find(int x)  // 如果查找元素存在，则返回对应下标；不存在则返回第一个空位的下标
{
    int u = (x % N + N) % N;
    while(h[u] != null && h[u] != x)
    {
        u++;
        if(u == N)  u = 0;
    }
    return u;
}

使用开放寻址法，哈希数组一般会开成数据规模的2~3倍，以减少冲突的概率。此外，如果使用开放寻址法发生TLE了，可能是哈希数组开小了所有的元素都用完了。

为什么使用0x3f3f3f3f来表示无穷大？》 C++中memset()函数的用法详解-CSDN博客

C++ STL的哈希表：

unordered_map<string,int> h;
h["123"] = 1;  // 插入
h["123"] = 2;  // 修改
h.erase("123");// 删除
//查找
h.count("123");

一般用STL就行，自己写也挺麻烦的

8.1 字符串前缀哈希

适用问题：用来解决多次查询一个字符串中子串哈希的问题

8.1.1 字符串前缀哈希法的步骤

(1) 计算字符串所有前缀字符串的哈希值

例如字符串S，该字符串从下标1，长度为n，将该字符串看作一个n位进制数，则该字符串的哈希值为：

该值可能非常大，因此还需要对一个较小的数字取模，在具体实现中使用unsigned long long 类型存储hash值，如果hash超过了该类型的最大数值，可以利用C语言的整型溢出机制自动对取模，即（后面的公式中会省略该取模步骤）

P一般取131或者13331，这是一个经验取值，99%的情况下不会发生冲突。

PS：可以直接使用字符的ASCLL值，也可以映射到其他数值区间。此外，不能将一个字符表示为数值0，例如假设字符A的值为0，那么字符串“A”和“AA”的Hash值相同，这显然是不可接受的。

(2) 计算字符串中任意子串的hash值

当计算出所有前缀字符串的哈希值之后，利用前缀和的思想即可计算出任意一段字符串S中任意一段字符串S[l,r]的哈希值：

我们需要将两个前缀字符串相同的子串部分在数值上对齐，从而确保计算出的hash值能够正确表达字符串s[l,r]的hash值，例如我们需要求字符串 cd 的哈希值：

8.1.2 示例代码

字符串哈希 - AcWing题库

代码：

#include <iostream>
using namespace std;
const int N = 100010, P = 131;
typedef unsigned long long ULL;
char s[N];
ULL h[N], p[N];

ULL find(int l, int r)  //计算任意子串的哈希值
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    int n, m;
    scanf("%d%d%s", &n, &m, s + 1);
    
    p[0] = 1;
    for(int i = 1; i <= n; i++)
    {
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + s[i];
    }
    while(m --)
    {
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if(find(l1, r1) == find(l2, r2))  puts("Yes");
        else puts("No");
    }
    return 0;
}

9.图的存储

图的存储可以使用邻接表或者邻接矩阵，邻接表一般用于存储稀疏图，邻接矩阵一般用于存储稠密图。

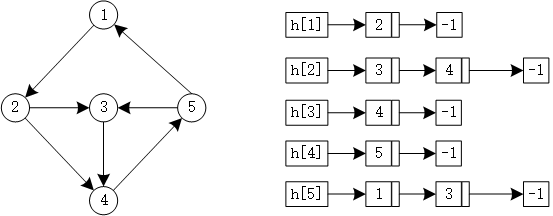
9.1 邻接表

使用数组模拟单链表的方式为图中每一个节点建立一个链表，在链表中存储该点所能达到的所有点。如下图所示：

示例代码：

int e[N], v[N], ne[N], h[N], idx;
void add(int l, int r, int w)
{
    e[idx] = r, v[idx] = w, ne[idx] = h[l], h[l] = idx++;
}

memset(h, -1, sizeof(h));
for(int i = 0; i < m; i++)
{
    cin >> a >> b >> w;
    add(a, b, w);
}

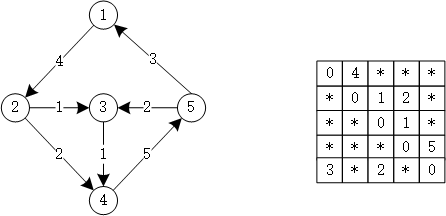
9.2 邻接矩阵

示例代码：

int g[N][N];
memset(g, 0x3f, sizeof(g));
for(int i = 1; i <= n; i++)
    g[i][i] = 1;
for(int i = 0; i < m; i++)
{
    cin >> a >> b >> w;
    g[a][b] = min(g[a][b], w);
}

9.3 拓扑排序

定义：

若一个由图中所有点构成的序列 A 满足：对于图中的每条边，都在中都出现在之前，则称是该图的一个拓扑排序

性质：

一个有向无环图一定存在拓扑排序并且一定存在入度为0的点（入度：指向一个点的边的数量，出度：一个点被指向的边的数量）

求拓扑序的思路：

记录各个节点的入度
将入度为0的节点加入队列
将队列中的点出队，遍历所有以该点为始的所有边，并将边所指向点的入度-1；如果所指向点的入度为0，则将其加入队列
如果所有点都进入过队列，则存在拓扑排序，输出队列中节点的出队顺序即为一个拓扑排序。否则，不存在拓扑排序。

代码：

使用数组模拟队列求拓扑排序，可以在求完之后直接输出队列数组中的元素。

int q[N], d[N];
bool topsort()
{
    int hh = 0, tt = -1;
    for(int i = 1; i <= n; i++)
        if(!d[i]) q[++tt] = i;
    
    while(hh <= tt)
    {
        int u = q[hh++];
        for(int i = h[u]; ~i; i = ne[i])
        {
            int v = e[i];
            d[v] --;
            if(!d[v])  q[++tt] = v;
        }
    }
    
    return tt == n - 1;
}

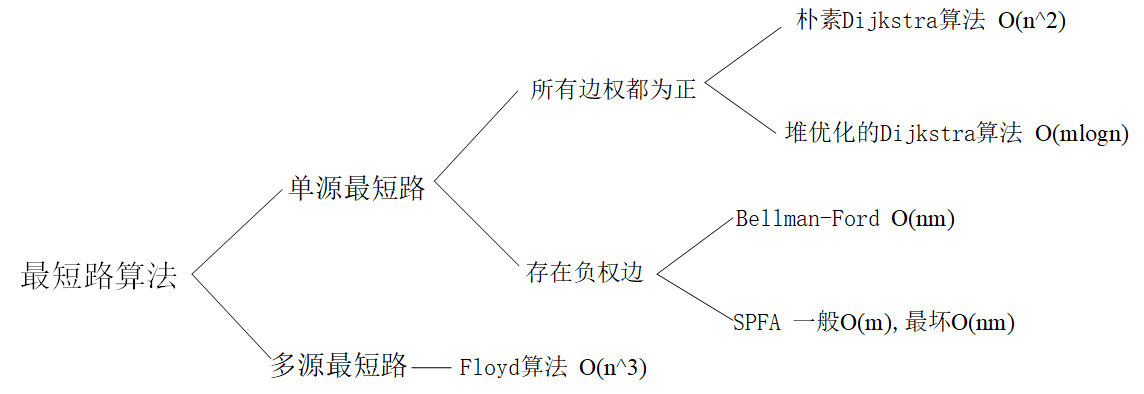
10.最短路算法

10.1 Dijkstra算法

10.1.1 朴素Dijkstra算法

时间复杂度：

适用于：无负权边，稠密图（）

算法思想：贪心

伪代码描述：

for point:1~n
	for point:1~n
		find 不属于集合S，并且dist[t]最小的节点t
	
	将节点t放入集合S
	
	for point:1~n
		dist[j] = min(dist[j], dist[j] + w[t][j])

集合为已知最短路径的节点的集合，如果图中包含负权边，则该结论不成立，因此Dijkstra算法仅适用于所有边权为正的情况。

算法模板：

int dijkstra()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    for(int i = 1; i <= n; i++)
    {
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        
        st[t] = true;
        
        for(int j = 1; j <= n; j++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

10.1.2 堆优化的Dijkstra算法

适用于：无负权边，稀疏图（）

伪代码描述：

while heap.size()
	{distance, t} = heap.top()
    heap.pop()
	
	将节点t放入集合S
	
	for all edge<t, b, w>
        if(dist[b] > distance + w)
            dist[b] = distance + w;
			if heap.find(b) is true
            	heap.update({dist[b], b})
            else
               	heap.push({dist[b], b})

时间复杂度：，每一个节点会遍历一次，每次会遍历该节点的所有边，而堆的插入时间复杂度为，因此总的时间复杂度为

算法模板：

int dijkstra()
{
    memset(dist, 0x3f, sizeof(dist));
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    
    heap.push({0, 1});
    while(heap.size())
    {
        PII t = heap.top();   heap.pop();
        int a = t.y, distance = t.x;
        
        if(st[a]) continue;  // 判重
        st[a] = true;
        
        for(int i = h[a]; ~i; i = ne[i])
        {
            int b = e[i], ev = v[i];
            dist[b] = min(dist[b], distance + ev);
            heap.push({dist[b], b});
        }
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

C++的STL对于堆的实现并不能实现修改或删除任意节点值的功能，因此我们将所有的{距离，节点}对都插入到堆中，并通过st数组进行判重，保证每一个节点仅会访问一次即可。

10.2 Bellman-Ford算法

时间复杂度：

适用于：负权图，求最多只经过k条边的最短路

伪代码描述：

for step: 1~n
    备份，用备份数组去去更新距离数组
	for all edges<a,b,w>
		dist[b] = min(dist[b], backup[a] + w);   （松弛操作）

算法性质：

第k次迭代后dist数组的实际含义：从源点出发经过不超过k条边，走到每一个点的最短距离
当算法结束后，对于任意一条边一定有（三角不等式）

算法模板：

struct {
    int a, b, w;
}edge[M];
int dist[N], backup[N];
int n, m, k;

int bellman_ford()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    
    for(int i = 1; i <= k; i++)
    {
        memcpy(backup, dist, sizeof(dist));
        for(int j = 0; j < m; j++)
        {
            int a = edge[j].a, b = edge[j].b, w = edge[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
    
    if(dist[n] >= 0x3f3f3f3f / 2) return 0x3f3f3f3f;
    else return dist[n];
}

Bellman-ford算法不需要建图，仅需要将所有边的信息保存下来即可。

10.2.1 判断负环

如果第n步迭代时，依然更新了某些节点的最短距离，则说明图中存在负环。spfa算法作为对Bellman-ford算法的优化，判断负环的方式是相同的。

简单证明：

如果第n次迭代更新了某些边的权重，说明存在经过n条边的最短路径，而n条边对应n+1个点，则说明最少有一个点相同，说明图中存在环；经过环反而能够更新权重，说明该环是一个负环。

PS：如果图中存在负权回路，则可能不存在到某些点的最短路

10.3 spfa算法

时间复杂度：一般，最坏

适用：比较通用，一般最短路问题都可以用spfa算法，除非出题人有意卡spfa。

spfa算法对Bellman-Ford算法的优化：仅有在一条边的起点的最短路被更新之后，更新这条边的终点的最短路才有意义。

因此，将被更新的节点加入队列，使用BFS的模板进行优化。

算法模板：

int e[N], v[N], ne[N], h[N], idx;
int dist[N];
bool st[N]; // st数组用于记录节点是否在队列中

int spfa()
{
    queue<int> q;
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;   st[1] = true;
    q.push(1);
    
    while(q.size())
    {
        int a = q.front();  q.pop();
        st[a] = false;
        
        for(int i = h[a]; ~i; i = ne[i])
        {
            int b = e[i], w = v[i];
            if(dist[b] > dist[a] + w)
            {
                dist[b] = dist[a] + w;
                if(!st[b])  
                {
                    q.push(b);   st[b] = true;
                }
            }
        }
    }
    return dist[n];
}

10.3.1 spfa算法判断负环

spfa判断负环的思路和Bellman-ford算法判断负环的思路一致，但是spfa不能明确的知道一条最短路径所经过节点的个数，因此需要额外开一个数组cnt，记录每一个节点当前最短路所经过的的节点的个数。

算法模板：

int e[N], v[N], ne[N], h[N], idx;
int dist[N], cnt[N];
bool st[N];

bool spfa()
{
    queue<int> q;
    //判断负环时，dist数组不要初始化，否则可能会爆int
    //初始化要将所有的节点都加入到队列中，防止子图不连通
    for(int i = 1; i <= n; i++)
    {
        q.push(i);
        st[i] = true;
    }
    
    while(q.size())
    {
        int a = q.front();  q.pop();
        st[a] = false;
        
        for(int i = h[a]; ~i; i = ne[i])
        {
            int b = e[i], w = v[i];
            if(dist[b] > dist[a] + w)
            {
                dist[b] = dist[a] + w;
                cnt[b] = cnt[a] + 1;
                if(cnt[b] >= n)  return true;
                if(!st[b])  
                {
                    q.push(b);   st[b] = true;
                }
            }
        }
    }
    return false;
}

10.4 Floyd算法

时间复杂度：

算法思想：DP

适用问题：边权可以为负，但不能存在负环，求任意一对节点之间的最短路（多源最短路问题）

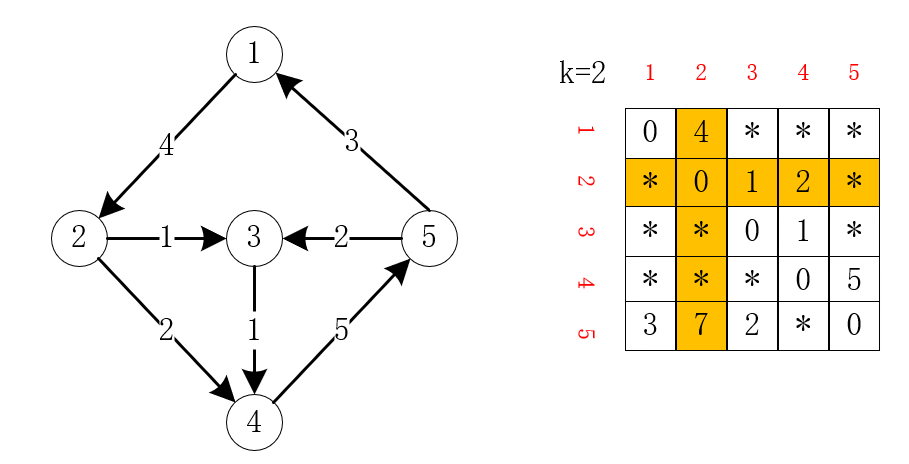
10.4.1 Floyd算法思路分析

状态表示：假设表示从这些节点中选择任意数量的节点作为中间经过节点时，节点到节点的最短距离。

状态转移方程：按照最短路是否经过节点进行讨论：

当最短路不经过节点时，
当最短路经过节点时，

合并两种情况，可得状态转移方程：

优化空间复杂度：

从状态转移方程中，可知第步时状态数组的值仅和第步时的状态数组有关，因此，最起码我们完全没有必要开一个三维数组，最多就足够使用
继续分析状态转移方程，看看能不能使用滚动数组的思想仅使用一个二维数组就能完成任务。以下图为例，图右表示经过步骤后得到的状态矩阵。可以发现每一个的值仅与自身和橙色区域的元素相关。当 $且$ 时，自身肯定是上一步得到的数值；当 $或$ ，自身就是橙色区域中的数值。也就是问题集中在于橙色区域的数值在本次循环中是否会更新。
可以证明不会：当 $或$ ，以为例，有：

由于图中不存在负环，则恒成立，因此上式可化为：

因此，当时，在第轮更新中，（横着的橙色区域）的值不会发生改变，为第轮中的数值。
综上，可以将状态转移方程简化为：

10.4.2 算法模板

int d[N][N];

memset(d, 0x3f, sizeof(d));
for(int i = 1; i <= n; i++)
    d[i][i] = 0;

for(int i = 0; i < m; i++)
{
    int a, b, w;
    cin >> a >> b >> w;
    d[a][b] = min(d[a][b], w);
}

void floyd()
{
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

11. 最小生成树算法

11.1 Prim 算法

时间复杂度：

适用于：稠密图

伪代码描述：

for point:1~n
	for point:1~n
		find 不属于集合S，并且dist[t]最小的节点t
	
	将节点t放入集合S
	
	for point:1~n
		dist[j] = min(dist[j], w[t][j])

和 dijkstra 算法比较相似，dijkstra 算法的 dist 数组表示每个节点到源点的最短距离。而这里的 dist 数组表示每个点到已知连通点集合的最短距离

算法模板：

int prim()
{
    memset(dist, 0x3f , sizeof(dist));
    dist[1] = 0; 
    for(int i = 1; i <= n; i++)
    {
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        
        if(dist[t] == 0x3f3f3f3f)  return 0x3f3f3f3f;
        res += dist[t];
        st[t] = true;
        
        for(int j = 1; j <= n; j++)
            dist[j] = min(dist[j], g[j][t]);
    }
    return res;
}

11.2 kruskal 算法

时间复杂度：

适用于：稀疏图

伪代码描述：

sort(edge:1~m)
for edge(a,b,w):1~m
    if a,b不连通
        将边m加入集合中

注：判断点是否连通使用并查集

算法模板：

struct Edge{
    int a,b,w;
    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edge[M];

int kruskal()
{
    sort(edge, edge + m);
    int cnt = 0, res = 0;
    for(int i = 0; i < m; i++)
    {
        int a = edge[i].a, b = edge[i].b, w = edge[i].w;
        int ua = find(a), ub = find(b);
        if(ua != ub)
        {
            p[ua] = ub;
            cnt ++;
            res += w;
        }
    }
    if(cnt < n - 1) return 0x3f3f3f3f;
    else  return res;
}

12. 二分图

二分图：指顶点可以分成两个不相交的集合，使得同一个集合内的点不相邻（没有共同边）的图

12.1 染色法判断二分图

性质：一个图是二分图当且仅当图中不含有奇数环

时间复杂度：

证明：

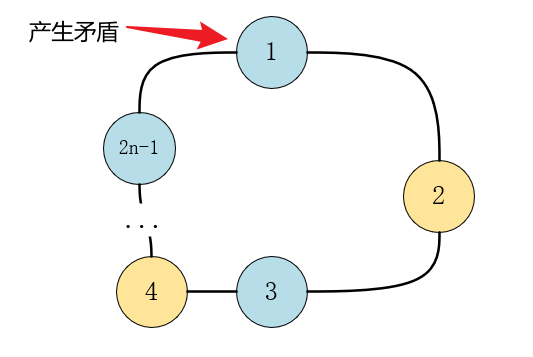
必要性：如果一个图是二分图，则该图中不含有奇数环。可以证明其逆否命题，如果一个图中含有奇数环，则该图一定不是二分图：

充分性：如果一个图不含有奇数环，则该图是一个二分图。可以利用图中不含有奇数环的性质，来对二分图中的点进行染色：通过遍历图的顶点，并将相邻的顶点分配到不同的集合来完成。确保相邻顶点分属不同集合，因为不存在奇数环，这样就可以满足二分图的定义。染色法采用的方式就是这样。

算法模板：

dfs 或者 bfs 均可，思路也比较简单。

bool dfs(int u)
{
    bool res = true;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int v = e[i];
        if(color[v] == -1)             // 未染色
        {
            color[v] = !color[u];
            res &= dfs(v);
        }
        else if(color[v] == color[u])  //染色冲突
            res = false;
        if(!res) break;
    }
    return res;
}

要注意有些图并非所有顶点全部连通，需要在 dfs 外增加一个循环来将每一个连通子图的某个顶点传入 dfs 中。

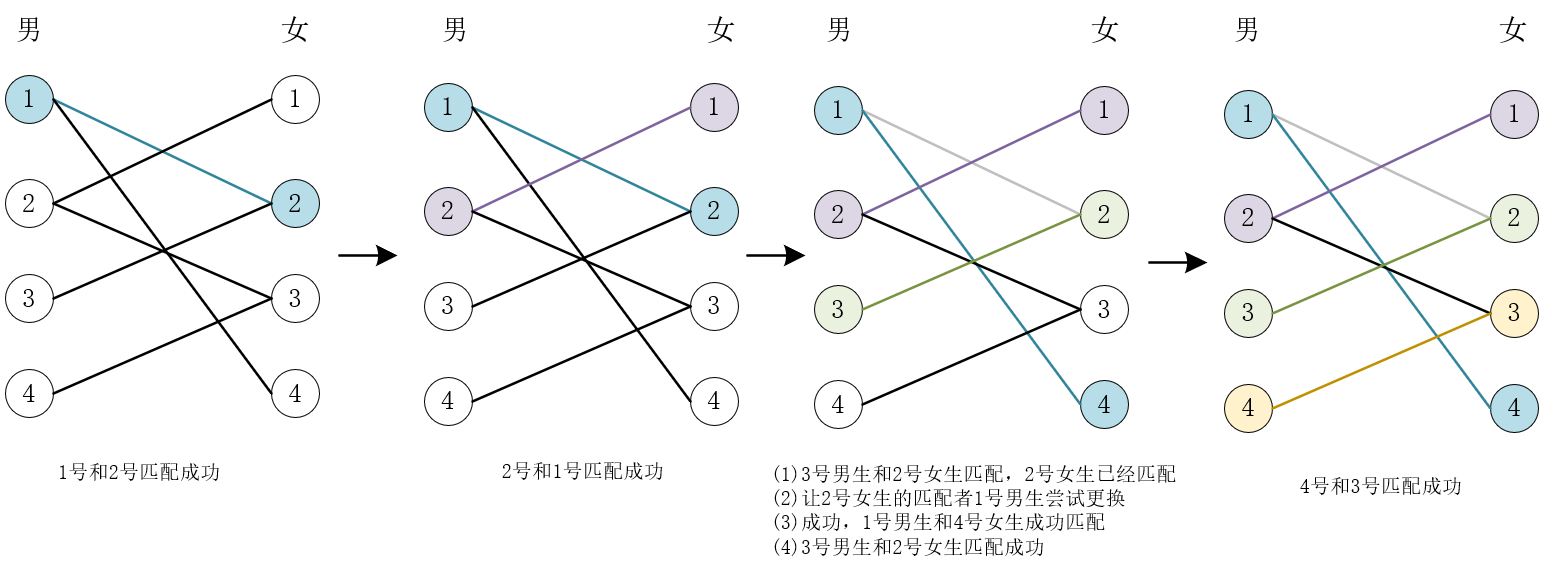
12.2 匈牙利算法求最大匹配数

二分图的匹配：给定一个二分图，在的一个子图中，的边集中的任意两条边都不依附于同一个顶点，则称是一个匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

通俗的来说，将二分图两边的顶点看作一群男生和一群女生，顶点之间的连线表示男生对女生有好感，一个男生可能对多个女生有好感，多个男生也可能对同一个女生有好感，我们要做的工作就是“拉郎配”，根据好感关系，使得这群男生女生中凑出最大数量的情侣关系（一对一关系）。如下图：

时间复杂度：，实际运行时间一般远小于

算法模板：

bool find(int u)
{
    for(int i = h[u]; ~i; i = ne[i])
    {
        int v = e[i];
        if(!st[v])
        {
            st[v] = true;
            if(!match[v] || find(match[v]))
            {
                match[v] = u;
                return true;
            }
        }
    }
    return false;
}

int cnt = 0;
for(int i = 1; i <= n1; i ++)
{
    memset(st, 0, sizeof(st));
    if(find(i)) cnt ++;
}

st 数组用来判断对于每一个左半部节点 u 寻找右半部节点的匹配时，是否已经判断过某个右半部节点 v，因此需要在进入 find 函数之前对 st 数组清零。